蒙地卡羅方法 - 從統計學到智慧型 AI 智能代理

蒙地卡羅方法（Monte Carlo Method） 是計算與統計領域中最強大且用途廣泛的工具之一。雖然它的名字讓人聯想到賭場策略，但其實這是一套嚴謹且極具實用性的隨機模擬方法，用來解決各種複雜問題。本文將介紹什麼是蒙地卡羅方法、它為何如此重要，以及它在遊戲人工智慧（如蒙地卡羅樹搜尋）與智慧代理中的應用。

什麼是蒙地卡羅方法？

蒙地卡羅方法是一類基於**重複隨機抽樣（random sampling）**來獲得數值解的計算演算法。核心思想是：透過大量模擬實驗來逼近實際結果，尤其是在解析解不可得的情況下。

換句話說，與其嘗試使用代數或微積分精確求解複雜問題，不如使用機率與統計的力量進行模擬與估計。

簡單範例

假設我們想用蒙地卡羅方法估算 π 值：

想像一個正方形中內切一個四分之一圓。
在正方形中隨機投點。
計算落在四分之一圓內的點數與總點數的比例。
此比例約為 π/4，乘以 4 即可估算 π。

為何在統計學中如此重要？

在統計學中，蒙地卡羅方法用於：

模擬機率分布：當分布無法用解析式表示時特別有用。
解高維積分：傳統數值積分法在高維空間效率低下，而蒙地卡羅方法則仍可適用。
風險分析與預測：例如財務模型中的不確定性模擬。
貝式推論：如 Markov Chain Monte Carlo（MCMC）在後驗分布取樣中的應用。

在人工智慧中的應用

蒙地卡羅方法在人工智慧中同樣扮演關鍵角色，尤其在不確定性處理、策略搜尋、與決策制定方面。

1. 蒙地卡羅樹搜尋（MCTS）

最著名的應用之一是 Monte Carlo Tree Search（蒙地卡羅樹搜尋），這是一種啟發式搜尋演算法，常用於策略型遊戲與決策系統。

MCTS 的工作流程：

MCTS 藉由模擬大量隨機遊戲進行來選擇最佳決策，其核心在於平衡：

探索（exploration）：嘗試新路徑以發現潛在好結果。
利用（exploitation）：傾向選擇過去表現佳的選項。

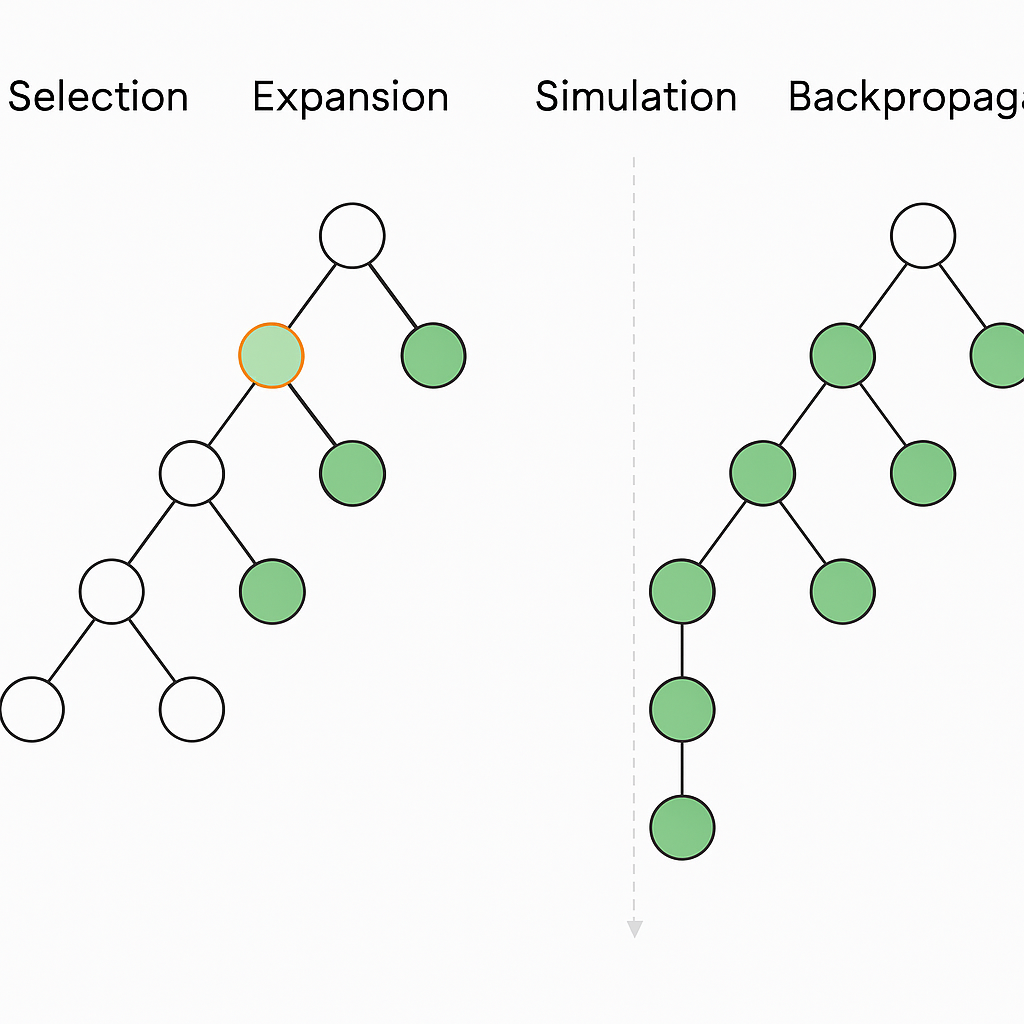
整體流程包含四個步驟：

選擇（Selection）：根據策略從根節點往下選擇子節點。
擴展（Expansion）：新增一個尚未擴展的子節點。
模擬（Simulation）：從該節點進行隨機遊戲模擬至終局。
回傳（Backpropagation）：將結果反向更新至路徑上的節點。

MCTS 是 DeepMind 的 AlphaGo 所採用的核心技術之一，幫助其在複雜的圍棋遊戲中擊敗世界冠軍。

2. 智慧型代理與規劃

在強化學習與智慧代理領域中，蒙地卡羅方法有以下應用：

估算回報值：透過樣本來估計策略的預期效益。
策略評估與改進：在未知環境下進行政策迭代。
部分可觀測馬可夫決策過程（POMDP）：透過蒙地卡羅模擬來進行信念更新與決策。

其他應用範疇

物理學：模擬粒子交互與能量分布。
金融工程：衍生品定價、風險模型。
機器人學：如蒙地卡羅定位（MCL）。
醫學：放射治療中的劑量分布模擬。

結語

蒙地卡羅方法的精妙之處，在於它將隨機性變為解題工具。當問題過於複雜、無法解析時，它提供一條可行的數值近似之路。從統計推論到智慧代理，從遊戲 AI 到財務模型，蒙地卡羅方法不僅是數學的藝術，更是現代科學與工程的基石之一。